Master Thesis: Diffusive Heat Transport Modelling for ASDEX Upgrade
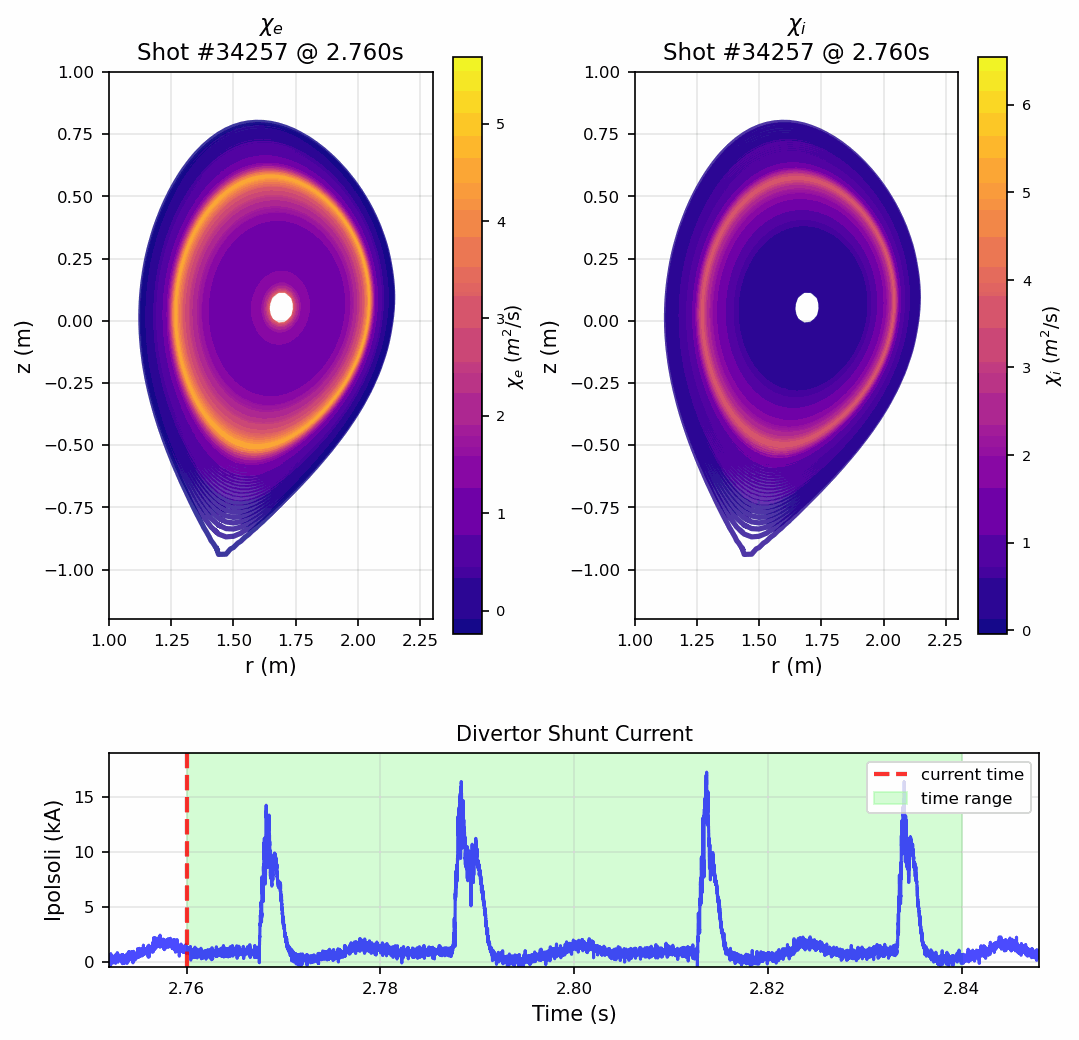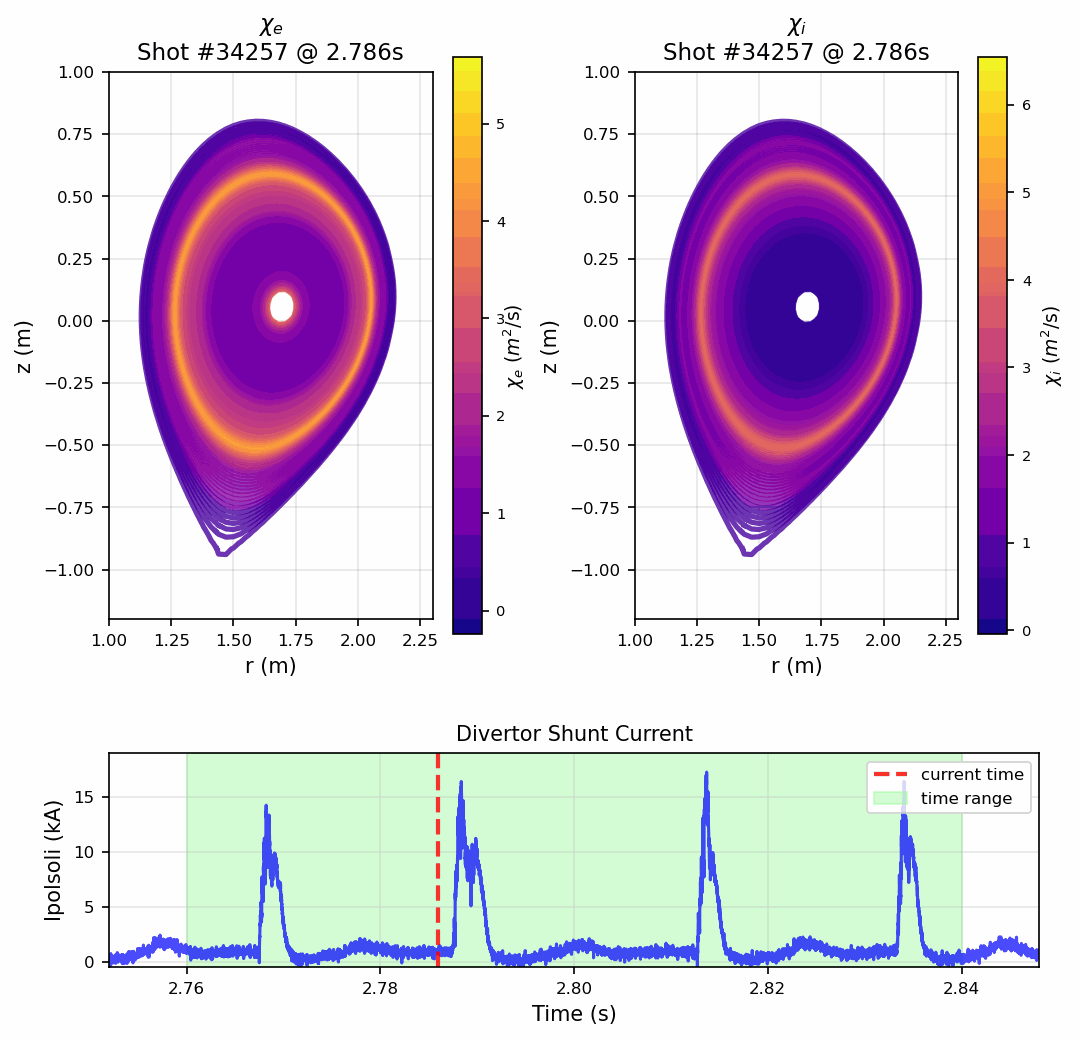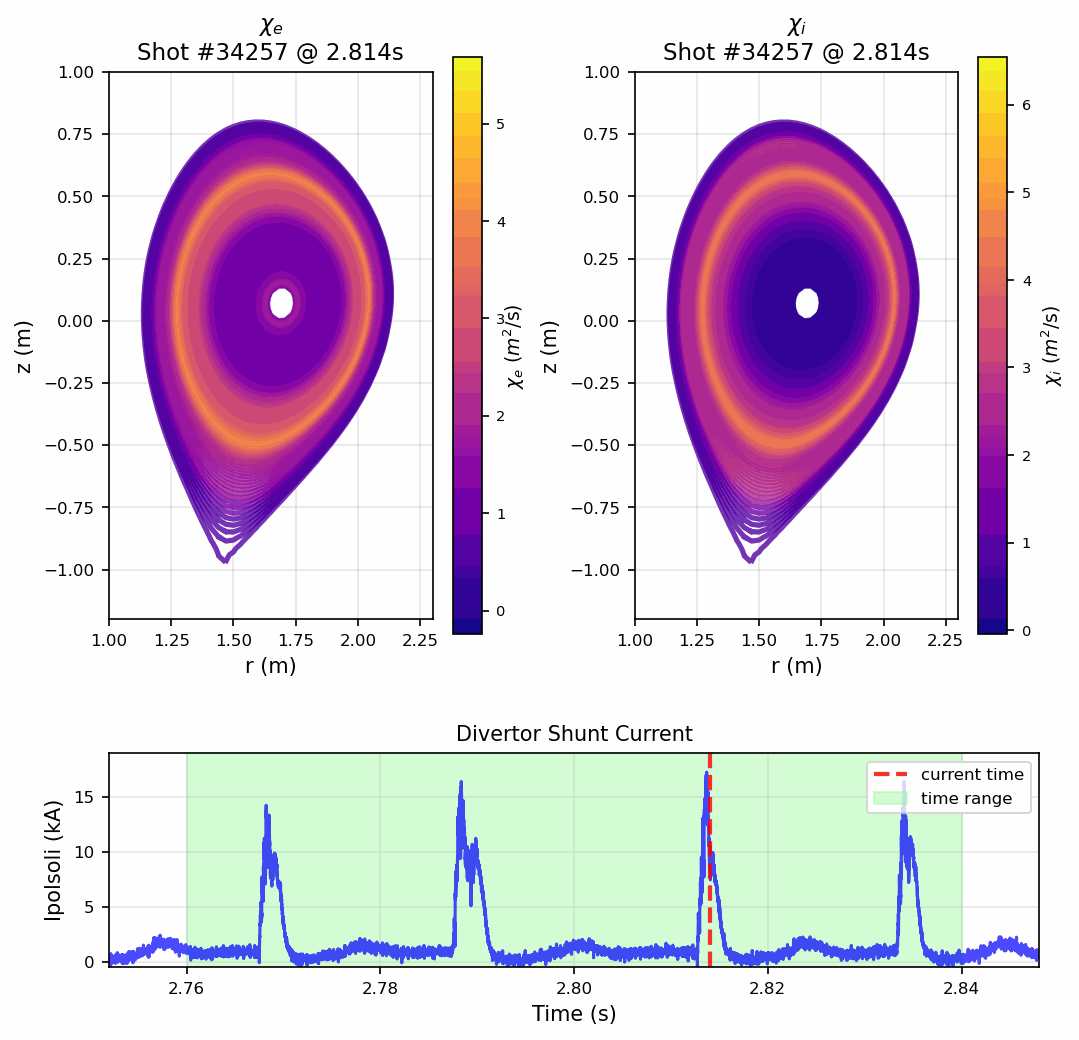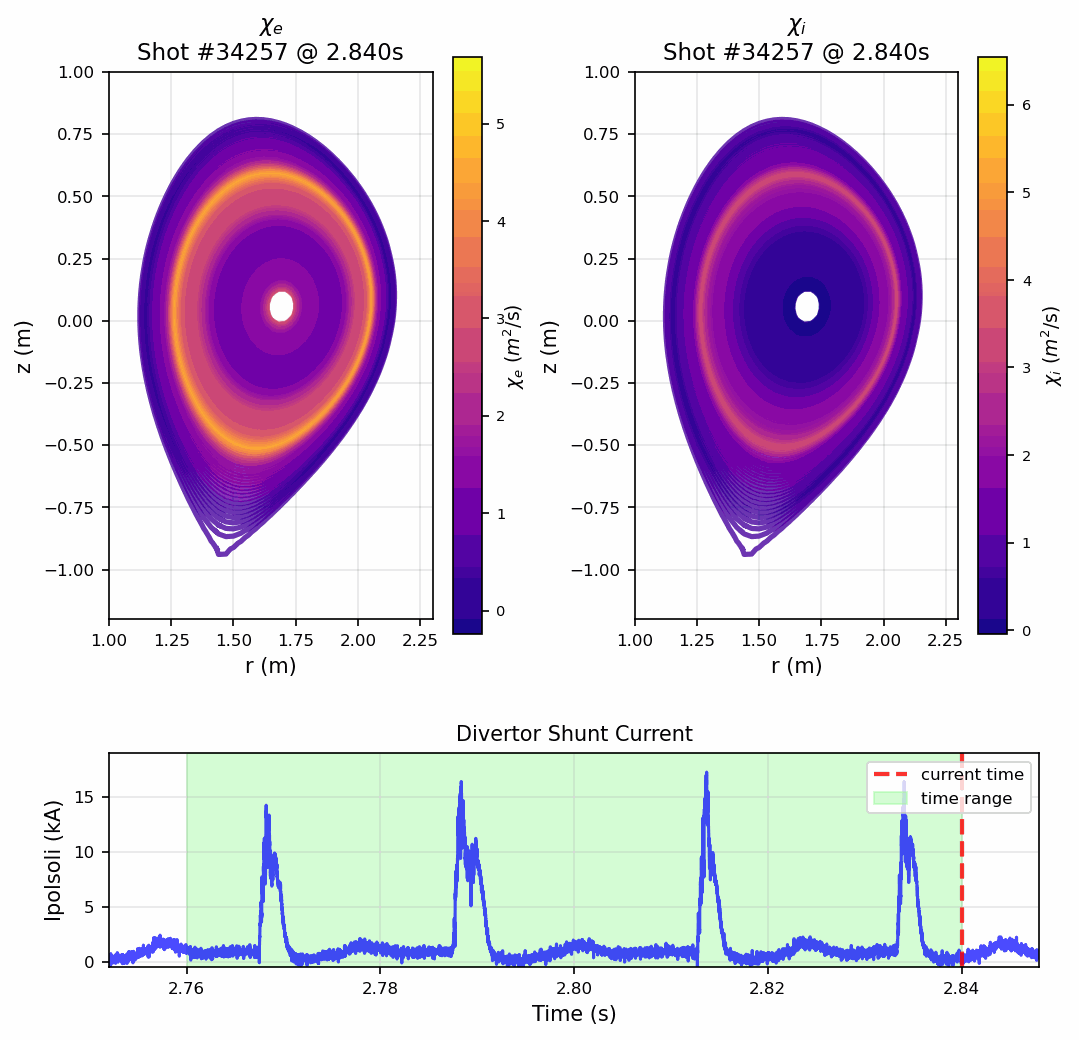
This master thesis tackles one of the most challenging problems in fusion energy: understanding how heat escapes from magnetically confined plasmas. In tokamaks like ASDEX Upgrade, turbulent transport dominates energy losses, making reliable heat transport estimates crucial for achieving net energy gain. Rather than relying on computationally intensive turbulence simulations, this work takes an innovative data-driven approach using exclusively experimental measurements. The thesis implements and validates a comprehensive heat transport analysis within the Bayesian Integrated Data Analysis (IDA/IDE) framework, calculating electron and ion heat diffusivities through detailed power balance equations. A major breakthrough is the development of a Gaussian Process Tomography (GPT) method for reconstructing radiated power profiles from bolometer measurements. This new approach, integrated directly into the IDE framework using Fortran90, features X-point-aware masking and advanced volume normalization techniques. The result is significantly more accurate transport coefficients, especially near the plasma edge where previous methods failed. The work includes comprehensive uncertainty quantification through Monte Carlo analysis and demonstrates the ability to resolve transport dynamics during Edge Localized Mode (ELM) cycles with high temporal resolution.
The Challenge
Fusion energy requires extremely hot plasmas (>100 million °C) to be magnetically confined for extended periods. However, turbulent transport causes heat to escape faster than classical physics predicts, threatening the goal of net energy gain. Understanding and predicting this heat loss is crucial for fusion reactor design, but traditional turbulence simulations are computationally prohibitive for routine analysis.
A Data-Driven Solution
Instead of relying on heavy computational models, this thesis develops a method that works directly with experimental measurements. By carefully analyzing power balance equations—accounting for all heating sources and energy losses—we can calculate heat transport coefficients that reveal how efficiently the plasma retains its energy. This approach makes transport analysis accessible for everyday use in fusion research.
Breakthrough in Radiated Power Reconstruction
A major innovation is the development of Gaussian Process Tomography for reconstructing how power is radiated throughout the plasma. Using advanced statistical methods on bolometer measurements, this new technique provides much more accurate results than previous approaches, especially near the plasma edge where transport is most critical for fusion performance.
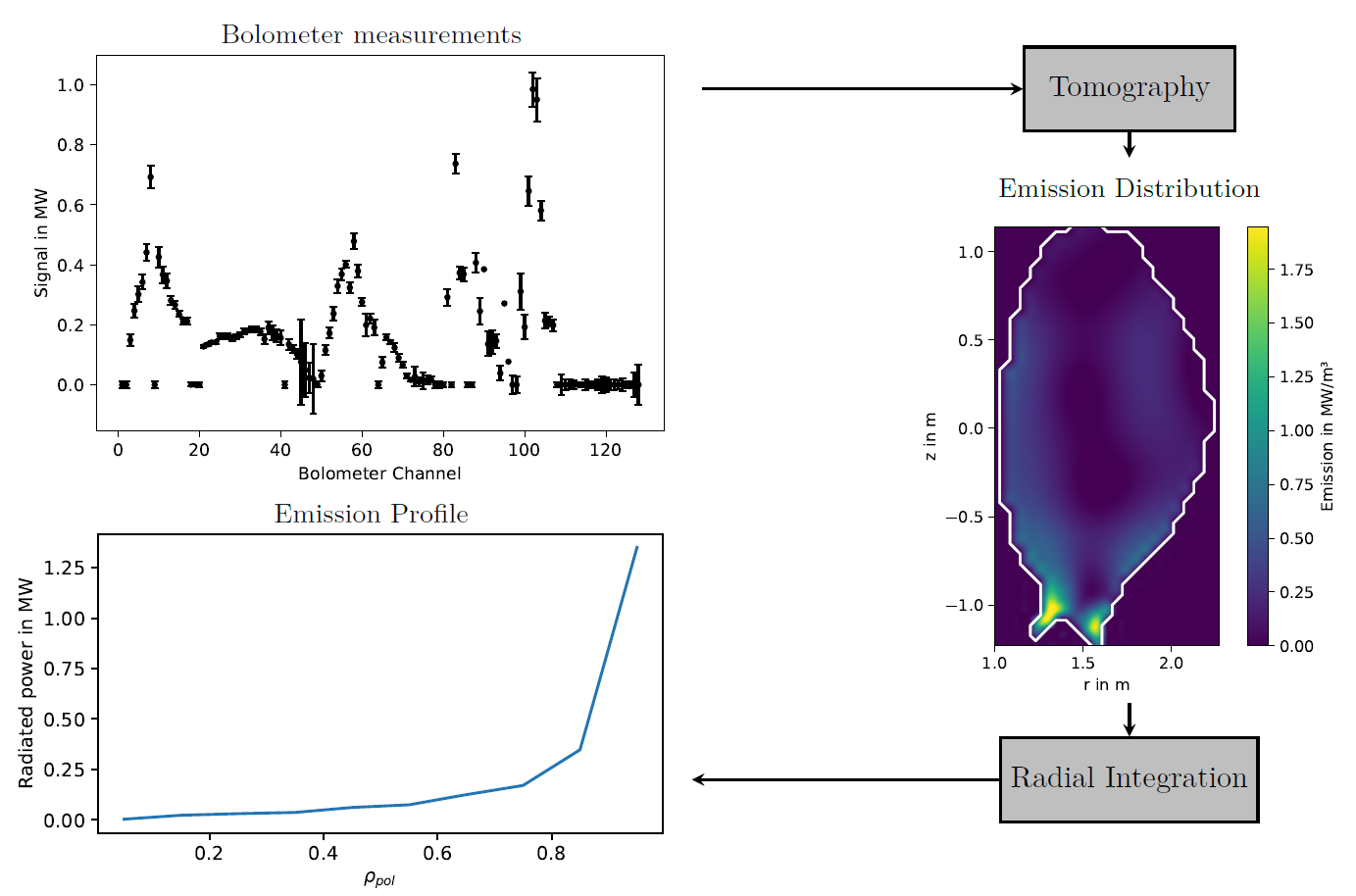
Uncertainty Quantification
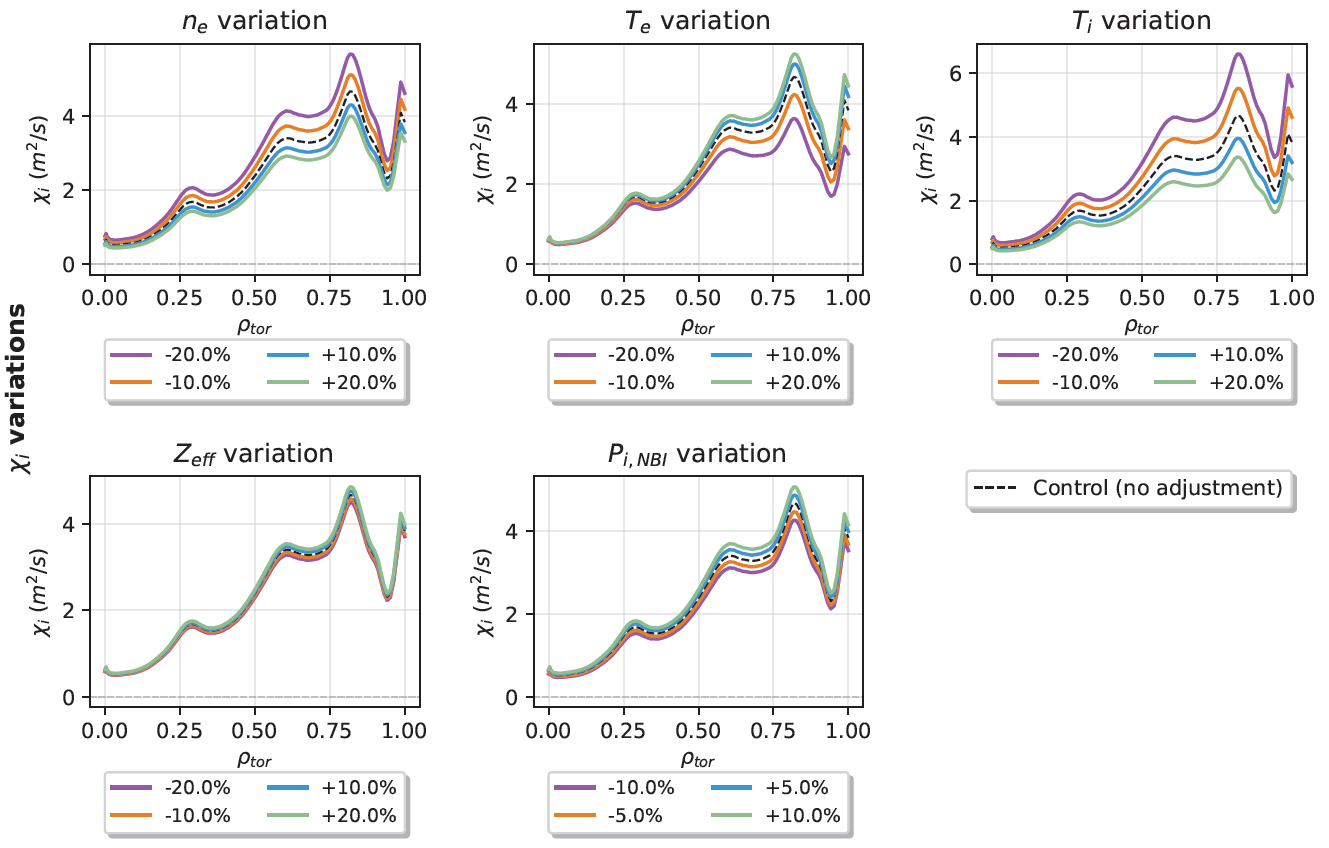
Understanding the reliability of our measurements is essential. Through comprehensive Monte Carlo analysis, the thesis maps out where our transport calculations are most trustworthy. Temperature gradients emerge as the dominant factor affecting accuracy, with the most reliable results occurring in the mid-radius region of the plasma (0.2 ≤ ρ ≤ 0.8).
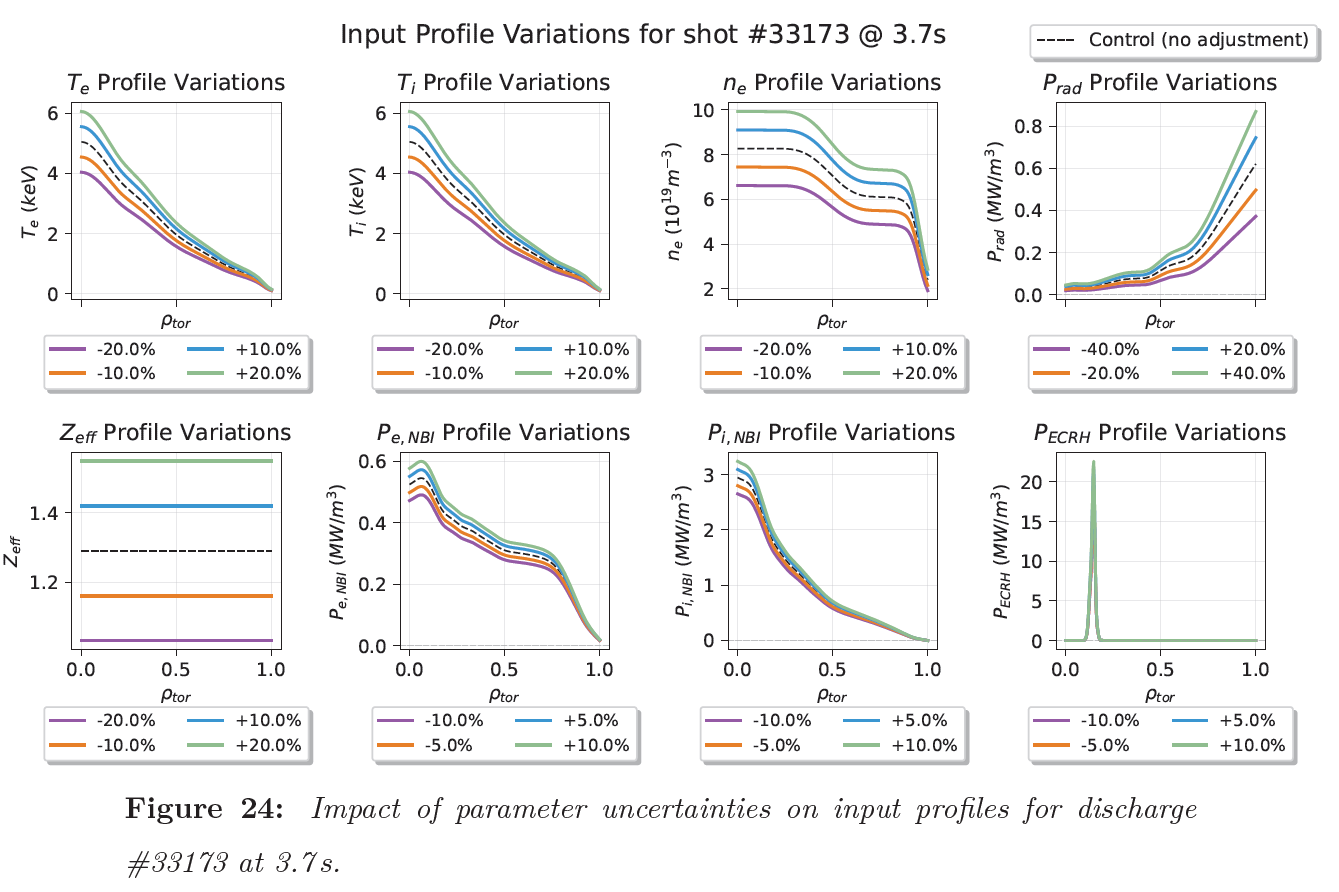
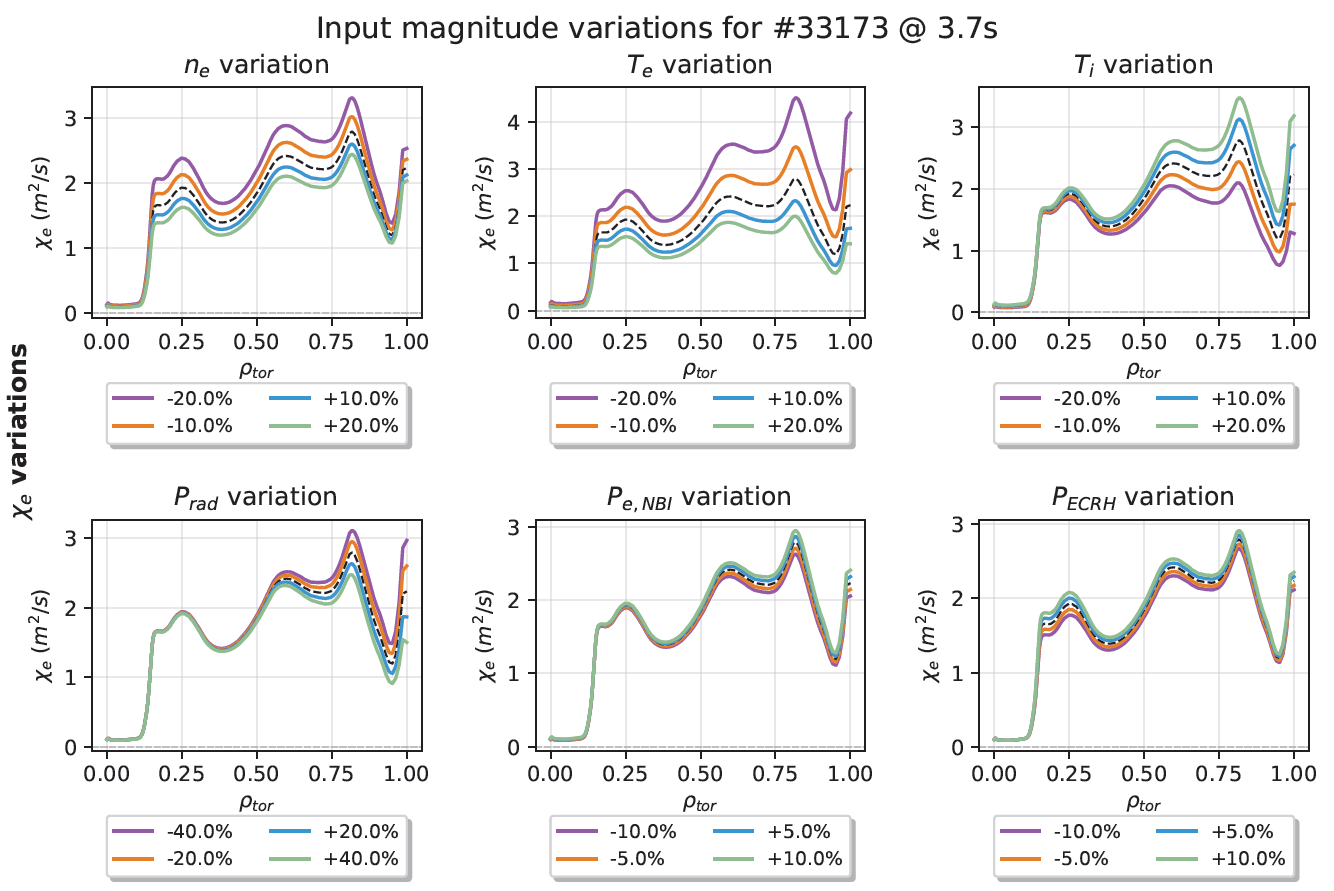
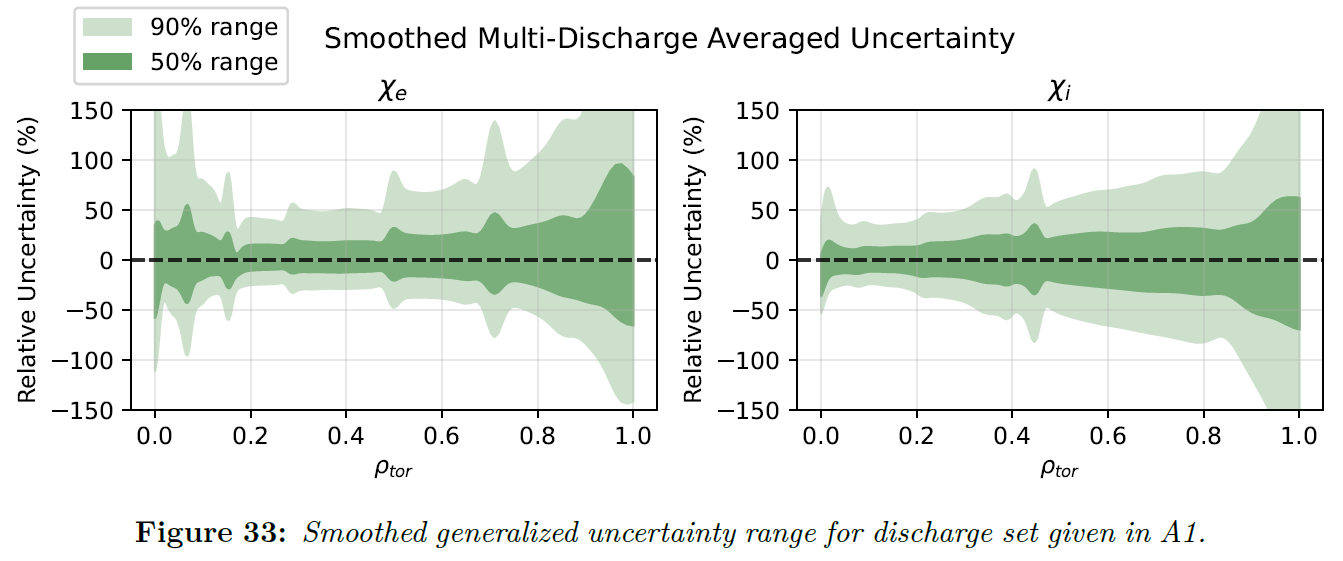
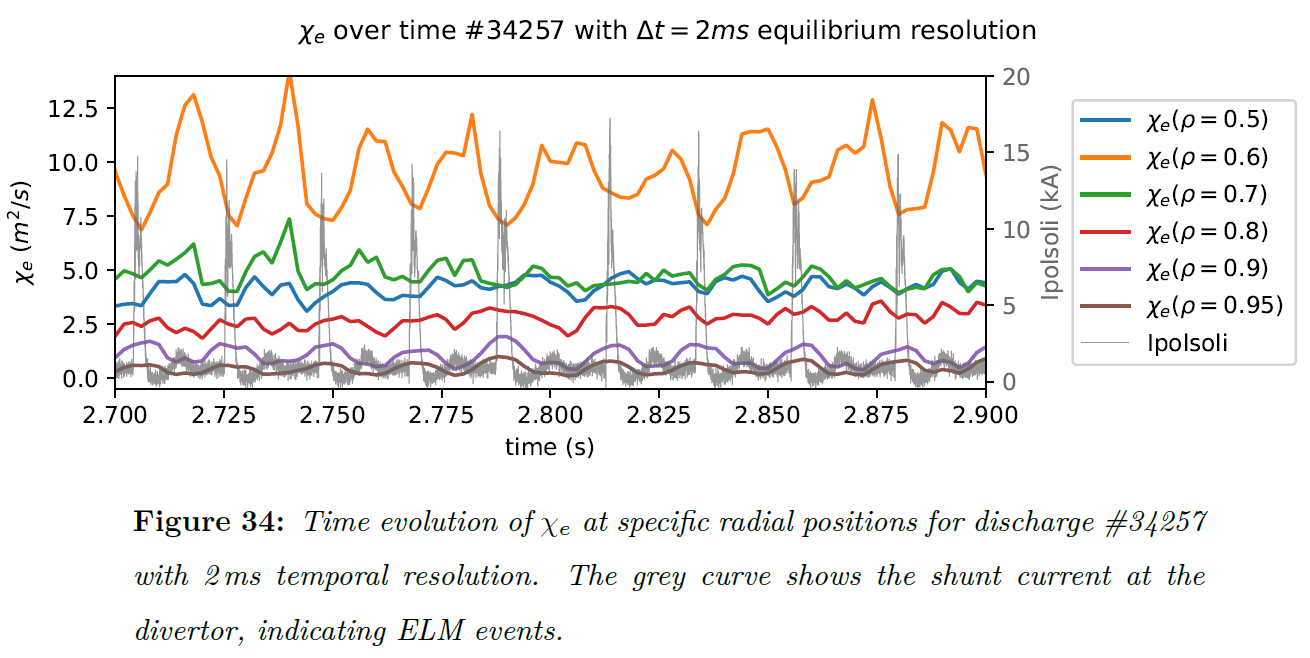
Capturing Plasma Dynamics
The method achieves sufficient temporal resolution to observe how heat transport changes during Edge Localized Modes (ELMs)—periodic instabilities that cause sudden heat bursts. This capability opens new possibilities for understanding plasma behavior and optimizing operational scenarios in real-time.
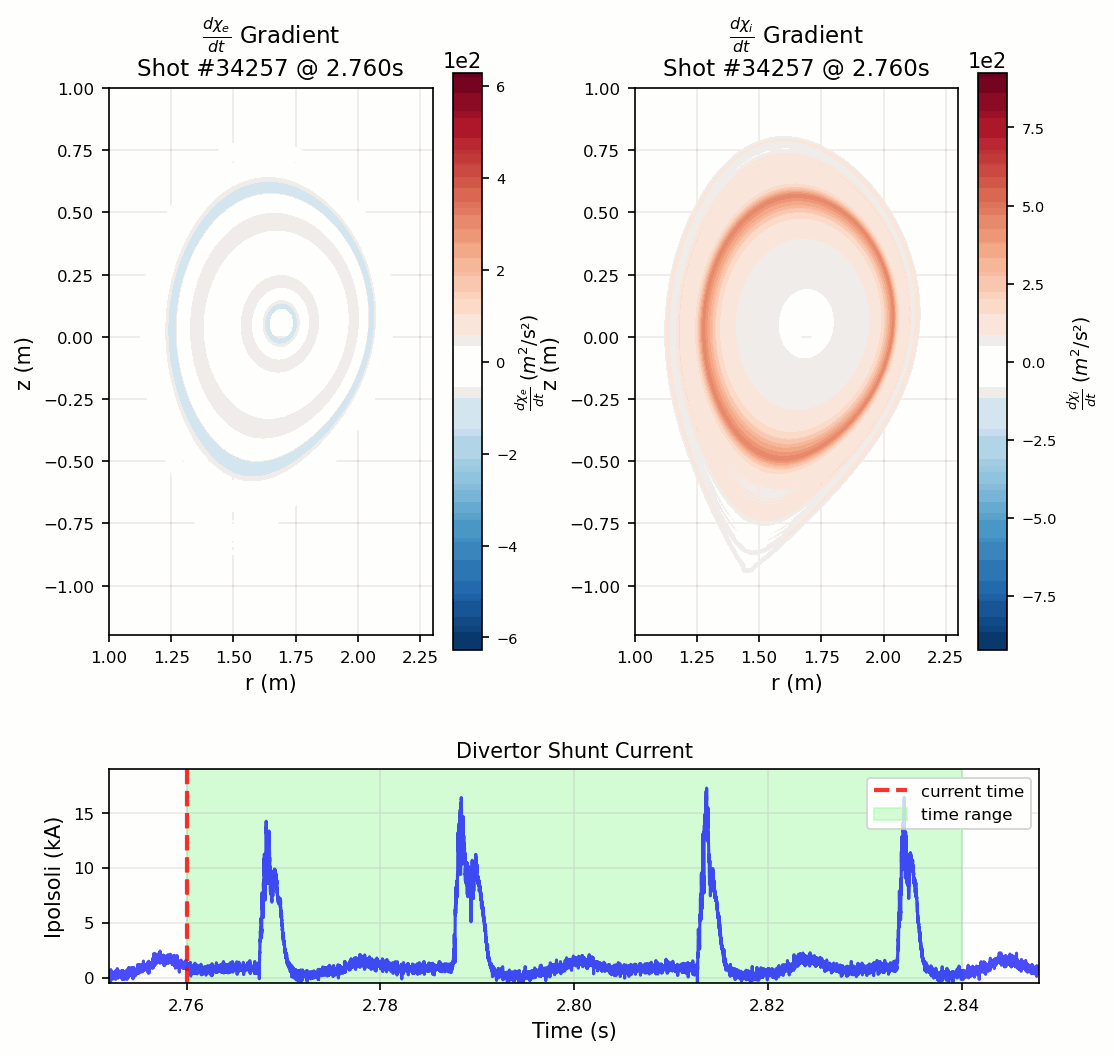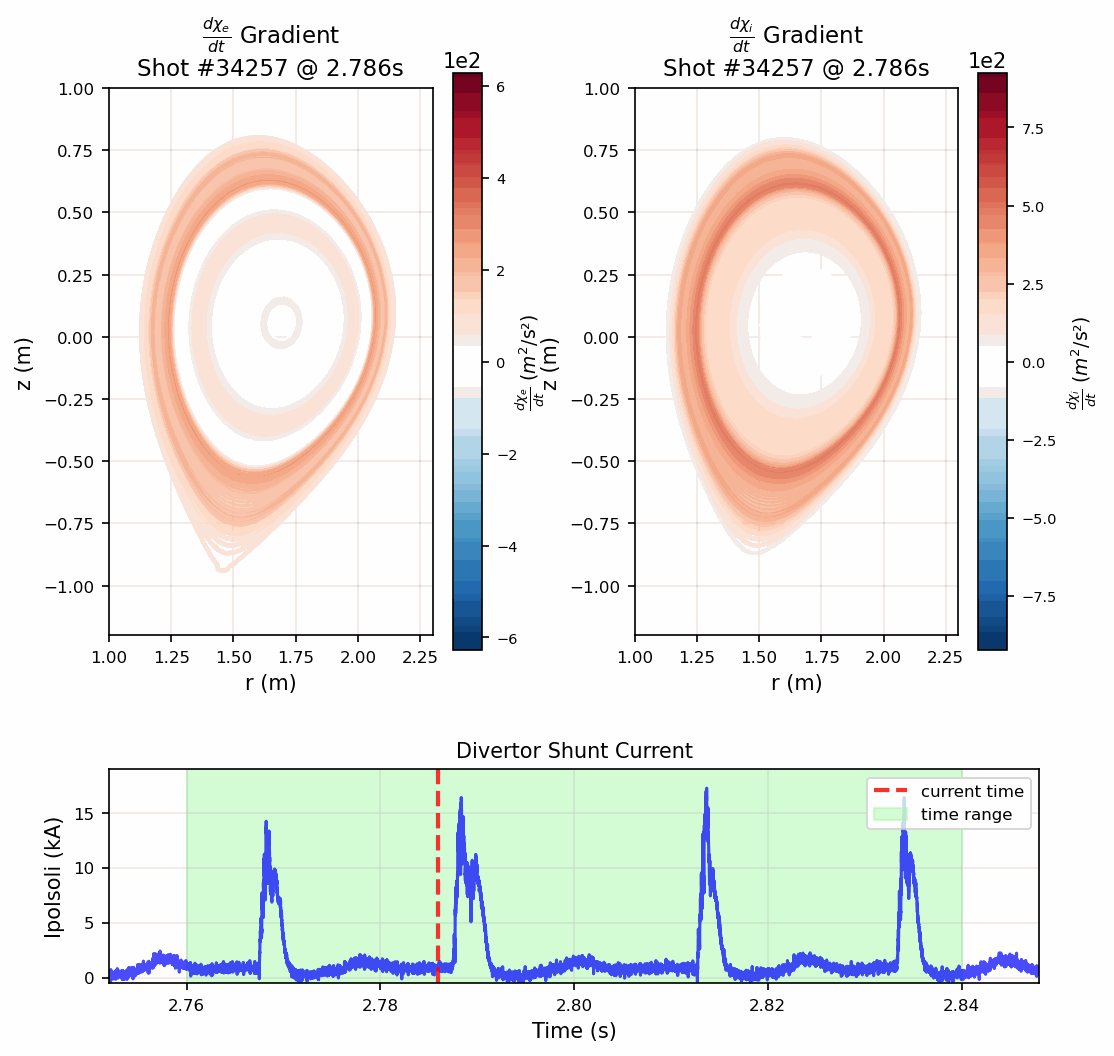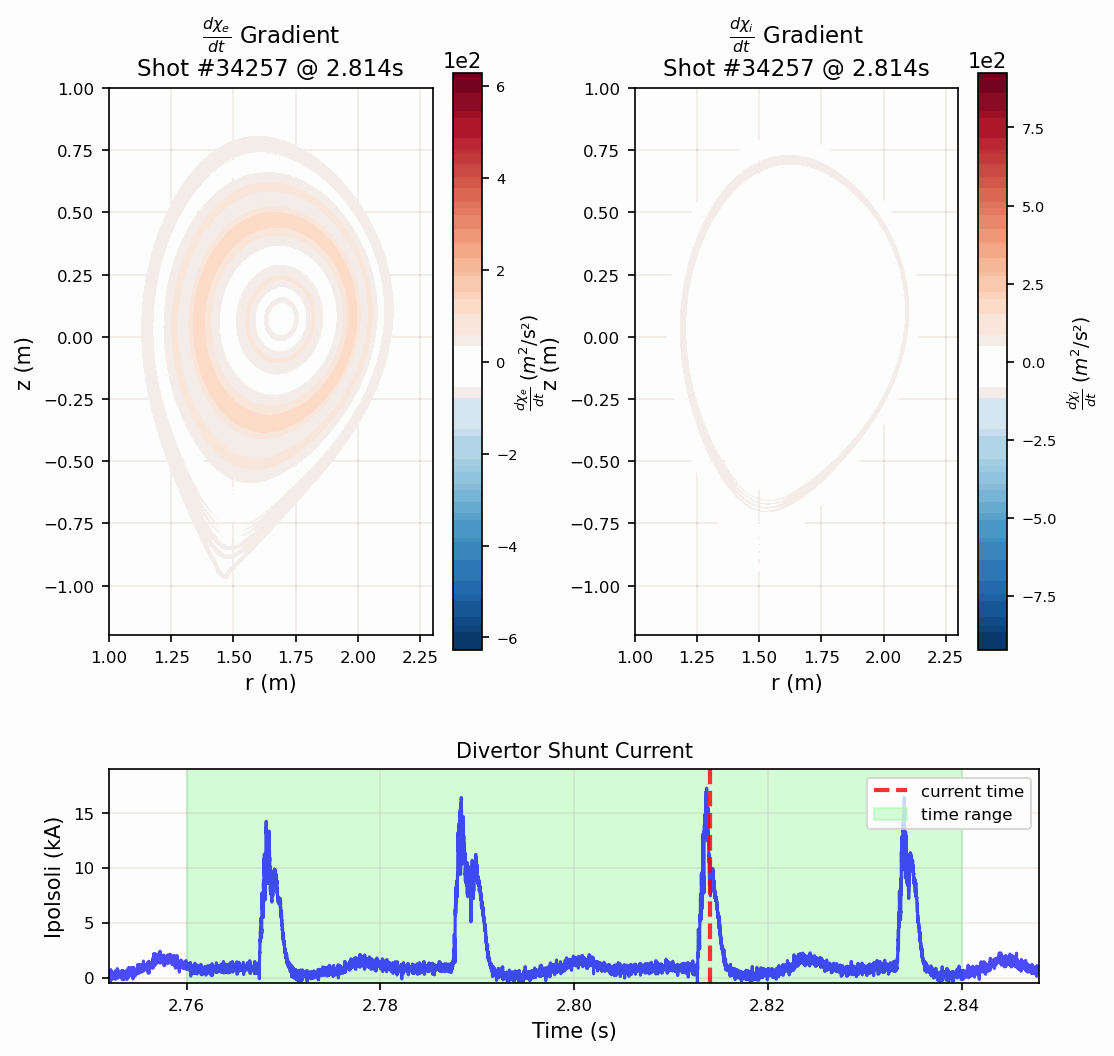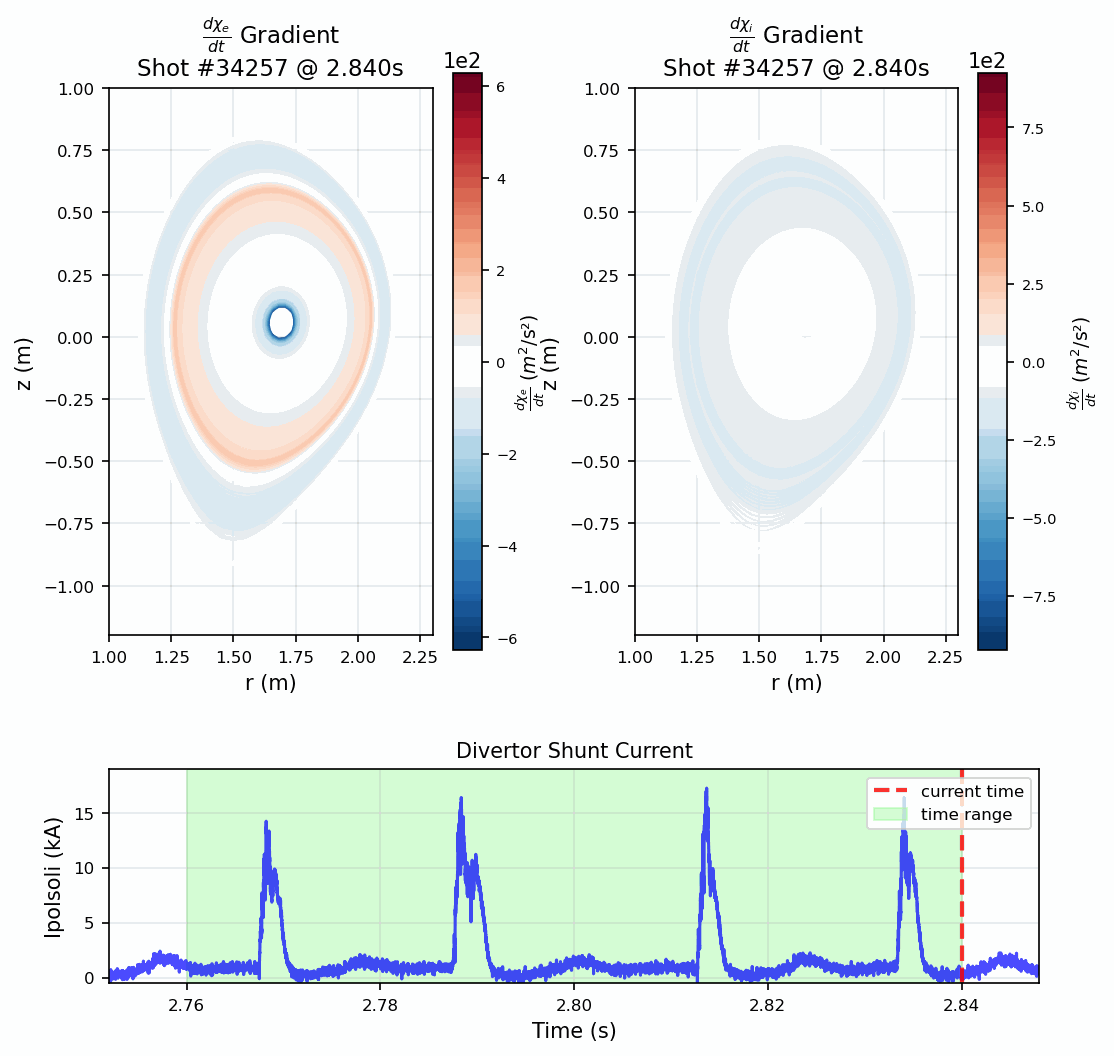
Impact and Future Applications
This work provides the fusion community with a validated, practical tool for routine heat transport analysis. Integrated into the ASDEX Upgrade analysis framework, it enables researchers to quickly assess plasma performance and inform scenario development. The approach could be extended to other tokamaks and adapted for real-time control systems in future fusion reactors.
Research Details
Conducted at TU Wien (Institute for Applied Physics) in collaboration with Max-Planck-Institut für Plasmaphysik, Garching. Supervised by Prof. Dr. Elisabeth Wolfrum, Dr. Rainer Fischer, and Dr. Michael Bergmann. The work combines advanced statistical methods with plasma physics expertise to address one of fusion energy's key challenges.
- 1Data-driven heat transport analysis using experimental measurements only
- 2Gaussian Process Tomography for radiated power reconstruction from bolometer data
- 3X-point-aware masking to exclude divertor regions while preserving plasma emission
- 4Advanced radial integration with spline-based volume normalization
- 5Comprehensive uncertainty quantification through Monte Carlo sensitivity analysis
- 6High-resolution temporal analysis revealing transport dynamics during ELM cycles
- 7Integration into Bayesian IDA/IDE framework for routine analysis
- •Replacing computationally intensive turbulence codes with experimental data approach
- •Accurate reconstruction of radiated power profiles from sparse bolometer measurements
- •Correcting unphysical edge roll-off artifacts from legacy radiation models
- •Implementing robust Gaussian Process methods in Fortran90 environment
- •Quantifying and propagating measurement uncertainties through complex calculations
- •Handling temporal resolution effects and dW/dt treatment in transient conditions
- •Validating results across different plasma regimes and operational scenarios
- •Power balance formulation for electron and ion heat transport in tokamaks
- •Advanced Gaussian Process techniques for sparse data reconstruction
- •Importance of proper geometric masking in plasma tomography applications
- •Statistical methods for uncertainty propagation in fusion plasma analysis
- •Temporal dynamics of heat transport during magnetohydrodynamic instabilities
- •Integration challenges between modern statistical methods and legacy codes
- •Practical considerations for making research tools available for routine operation